Fluon Theory (FLT)

Home

Visit this to see fluon art.

Fluogen is a program that generates fluon art.

You should also read about MDNT.

In the videogame Portal, portals are like fluons, so you can experience how it would be to travel through fluons.

Created by Gardener of Thoughts. Released under a Common Sense License.

Introduction

Math

Movement

Questions and answers

What is Reality?

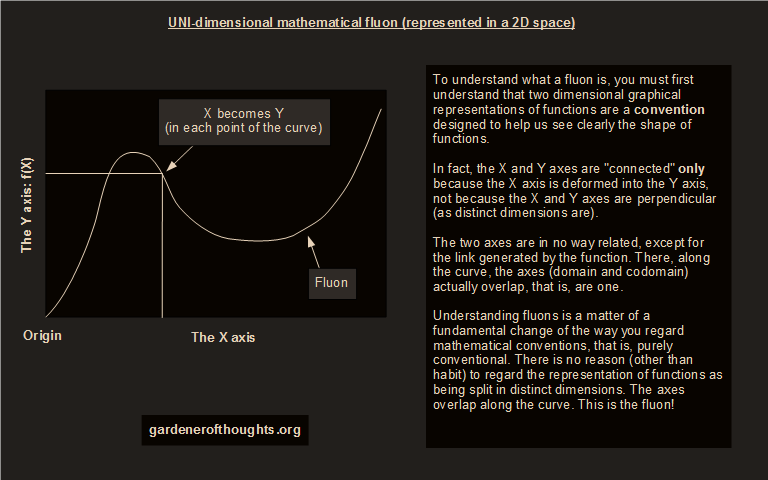
Introduction

The name "fluon" comes from the Latin "fluo" which means "flow" or "stream". This is meant to represent the fact that in a fluon, space flows smoothly from domain to codomain, through a remapped continuity within the same space.

The fluon theory is a mathematical view which separates the abstractions from the conventions (= intuitive representation) of what the mathematical space is.

In the widest and most abstract interpretation, a fluon is the application / representation of a mathematical function from domain to codomain. The domain is an abstract coordinate space where there is nothing other than distances, in which an equation is applied to produce the codomain. The codomain appears to be more than an abstract coordinate space, especially when the equation is a progression. The codomain appears to manifest, to have presence, to behave like a substance, because the distribution of the coordinates changes.

In a narrow interpretation, the fluon theory describes how domain-codomain continuity is being remapped by equations.

To understand what a fluon is, you must make a fundamental change in the way you regard mathematical conventions, that is, purely conventional. For this, you have to understand that two dimensional graphical representations of functions are a convention designed to help people see the shape of one dimensional functions.

Let's say that if you were to apply a function in a 1D space, you would get a result in a 2D space. But then, if you were to apply a function in a 3D space, would you get a result in a 6D space? Wouldn't this 6D space conflict with a 6D space that you could apply a function to? Why would space dimensionality grow as you scale your function? The only reason: conventions.

In a 1D space, the X and Y axes (= domain and codomain) are "connected" only because the X axis is transformed into the Y axis, not because the X and Y axes are perpendicular (as actual dimensions are). The two axes are not axes in a 2D space, they are in different spaces, domain and codomain, and are linked by a function application / representation.

But can we really say that the domain and codomain are separate spaces? Maybe in an abstract realm we can, but consider the example of moving an object in space with 1 meter on the X axis. What really happens in such a case? A translation equation in the form Y = X + 1, where the domain and codomain are the same space, a space where the Y axis overlaps the X axis, so the mathematical convention of having perpendicular axes went away. We can say that along the function's application / representation, the axes overlap. The application / representation of a mathematical function from domain to codomain, in the same space, is the fluon.

Here is a graphical example (the OpenDraw file is here):

As a practical application, an object can move from one point to another (in an D-dimensional space) without passing through the space in between, but rather skipping all that and moving as if through a door because the continuity of the space is remapped.

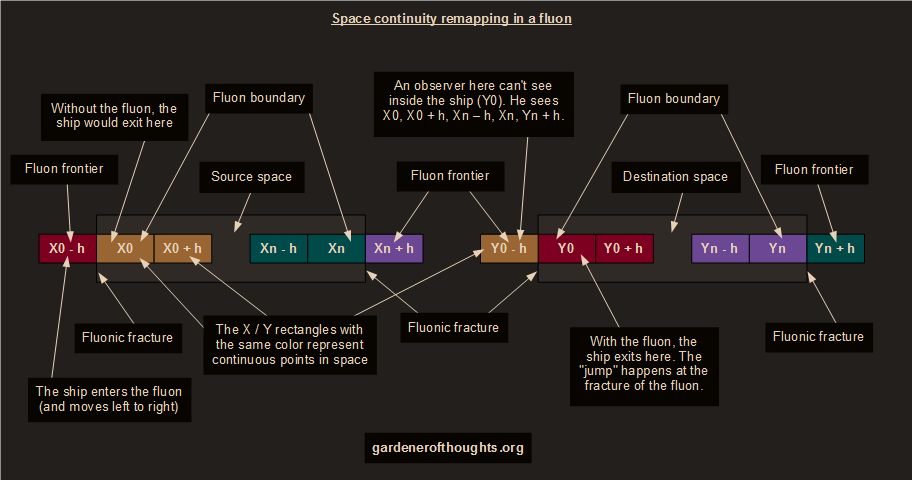
Math

By applying a function on a MDN{D} space S, its continuity is remapped to another MDN{D} space D (situated at any distance from space S). The function which is applied on space S is called fluonic function, and it creates a link between space S and space D as if there is no other space between them. Here is a graphical example (the OpenDraw file is here):

Space S is defined from x0 to xn, where n is any integer bigger than (or equal with) 0. Space D is defined from y0 to yn. The fluonic function is defined as yk = f(xk), where k is any integer between 0 and n.

The MDN{D - 1} space which wraps around space S (or D) is called fluonic frontier. For space S this is x0 - h, x0 + h, xn – h, xn + h (for space D this is y0 - h, y0 + h, yn – h, yn + h), where h tends to 0.

The MDN{D - 1} space which bounds space S (or D) is called fluonic boundary. For space S this is x0 and xn (for space D this is y0 and yn).

A mathematical discontinuity which occurs between the frontier of space S (or D) and the boundary of space S (or D) is called fluonic fracture. For space S this discontinuity is between the pairs x0 – h and x0, x0 + h and x0, xn – h and xn, xn + h and xn (for space D this is between y0 – h and y0, y0 + h and y0, yn – h and yn, yn + h and yn).

Although space S and space D are discontinuous in the place of their fluonic fractures, space S-D is continuous. The continuity of the common space is remapped between the frontier of space S (or D) and the boundary of space D (or S). The continuity of the space S-D is bidirectionally remapped from x0 – h to y0 to y0 + h, from x0 + h to x0 to y0 – h, from xn – h to xn to yn + h, from xn + h to yn to yn – h.

The continuity is not remapped inside space S (or D).

The two spaces S and D, together with their frontiers, boundaries and fractures, form a fluonic space, also known as fluon.

If after the application of a fluonic function on space S, all the points from space S and space D have identical relative positions, and are bound by a fluonic fracture but are not traversed by any other one, the generated fluon is called coherent, else incoherent.

In a fluon, an object which is within space S (or D) is not in two places at the same time. The continuity of the spaces has been remapped, but the spaces remain independent. Jumping from one space to the other occurs only at the fluonic fractures, not inside space S (or D).

Movement

The movement of objects through space (including through fluons) is a continuous movement.

The movement through a fluonic fracture is seen by an external observer like a jump in space; the jump occurs only at a fluonic fracture, not inside a fluon. However, for the moving object there is no jump because the remapped space (of the fluon) is continuous.

If a fluonic function y = f(x) is applied in point x then an object can't travel from x - h to x + h because of the discontinuity between x – h and x, and between x and x + h. However, the object can travel from x - h to y and then to y + h. When the object reaches y, it is at the destination of the travel.

The direction of the movement of an object through a fluonic fracture corresponds with the way the points of the domain (space S) and codomain (space D) of the fluonic function correspond with each other.

If the fluon is a MDN{D} zone in a MDN{D} space (like a sphere in a 3D space), the "jump" occurs both when an object enters in the sphere and when it exits (or just when the object exits the sphere, if the object was inside the sphere when the fluon was created). This means that if there are any natural thin fluons, an object can't disappear somewhere else in space because it would go through both fractures of the fluon (and would thus remain at the source location). This is the reason why we don't have much chances to move through a natural fluon and remain at the destination.

For an object to remain at the destination location, it must move inside the fluon and fit entirely in it and then the fluon would have to be closed. Another way is for a fluon to be created around an object, and then the object would have to move outside the fluon so that the object could "jump" to destination. Here is a graphical example (the OpenDraw file is here):

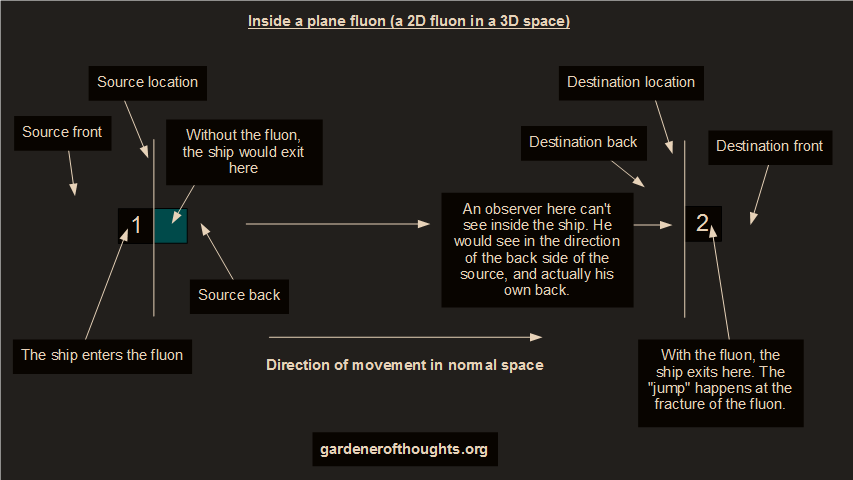
If the fluon is a MDN{D - 1} zone in a MDN{D} space (like a plane in a 3D space), an object would remain at the destination location if it would simply move through the fluon. Here is a graphical example (the OpenDraw file is here):

Questions and answers

What is a fluon?

Fluons are not about something new (like particles), but about a different way to look at mathematics. In mathematics, you can apply a function on a point and associate a different value to it; you know, each X has an Y associated. Point X actually becomes another point Y by applying a function on it.

The real / physical space manifests "features" like mathematical functions: points from it can become other points. To understand this, one has to simply translate the mathematical vision in real space, but by thinking that the X and Y axis overlap (instead of forming a 2-dimensional space like in any mathematical representation of a function). Of course, the manifestation of fluons in reality is pure speculation. The fluon theory is purely mathematical.

What is a fluon good for?

Fluons can be used for transportation from one place to any other place, without any distance being traveled, like walking through a door.

How would a fluon be created?

Probably some sort of electromagnetic or gravitational field can be used to apply some mathematical function (= the fluonic function) in the real space, like Y = f(X), and that the continuity between the space X (the source location of the travel) and space Y (the destination location of the travel) is remapped in the real / physical space, that is, the space which surrounds space X becomes continuous with space Y.

The origin point of the space is also generated by the fluonic function.

How would space travel work?

Fluons can be used for instantly jumping from anywhere to anywhere, regardless of the distance. Still, there are things which may make such jumps perilous.

Most likely, some sort of some device would be used to create some sort of doors to various locations, at any distance. The difference between this type of door and wormholes is that there is nothing between the two locations linked by the door (like is hyperspace in the case of wormholes). It's just a door. It's like you would look / walk through a door and on the other side is a star / planet which is normally 1 million light years away.

Such a device doesn't consume more energy if the distance between the two points linked is increased. However, it may have one parameter called "positioning error" which results from calculation errors, so it may increase proportionally with the distance.

The positioning error refers to the inability of the device to create a door to the exact specified destination coordinates. Instead, the destination is randomly positioned inside some sphere around the specified destination coordinates; the radius of the sphere is the positioning error. This way, the actual destination coordinates are not precisely know before the jump is made, but only after.

This this kind of door doesn't have the usual problem of jumping into stars (and planets) because there is a certain energy required to create the door. If at the destination there is some dense object (which compresses the space), more energy is probably required to open the door.

The device probably requires significant energies to open the door near stars and planets (due to their gravitational fields which "press shut" the door). It's also possible that if the jump is performed close to stars / planets, the positioning error increases.

Can you help me visualize space travel?

To have a clear image of the process, imagine that you create a spherical fluon around a ship. This fluon links to another place in the Universe, of identical size and shape. Then, you move your ship out of this sphere, with 100 km/h. If this sphere is only imaginary, you would exit the sphere still at the source location. However, if the sphere is a fluon, you would exit through the same area but at the destination.

Unfortunately, using a 3D fluon in the Universe's 3D space means that the ship would end up still at the source location after it exists the sphere because it crosses two fluonic fractures (= the in-out edges of the spheres). This is because the actual jump happens at the 2D edge of the 3D sphere, edge called fluonic fracture.

While the ship is inside the sphere, it actually exists in both locations at the same time.

Now imagine that the fluon is a very thin circle. You move the ship through it and when it's half way in you would have two parts of your ship in two zones of the Universe: half at the source location, half at the destination. It's like your ship is broken in two, but it's not really broken because the space of the fluon is continuous. Note that if the destination location is behind your ship, you would actually exit behind your source location, but your ship would preserve it's direction (or if the fluon is shifted at 45 degrees you would have a 45 degrees change in the direction).

Do objects which move through a fluon remain intact?

Fluons can change the density of space at their frontier, and this can lead to the destruction of anything that moves through them.

Incoherent fluons do distort the objects which pass through them, but if the fluon is only slightly incoherent, it may regain its initial form because of the elastic forces within it.

Real fluons probably can't be created with absolute precision, that is, each micron from the source location is not mapped exactly into another micron at the destination location. If there are strong electromagnetic or gravitational forces near the source or destination locations of fluons, this problem could be increased.

What happens if a fluon closes while a ship is part inside and part outside the fluon?

The object could be severed where the fracture of the fluon is. However, it is possible that the fracture would not close because the object opposes a certain force.

What happens if I move through space and encounter a tinny fluon? Would I be sucked in?

Depends on the fluon. In most cases, nothing would happen because what would enter in the fluon through one fracture would get out through the opposite fracture, in the same location, like the fluon wasn't even there.

In the nasty, but rare cases, the fluon would act like a pin, that is, if you move toward it and keep going, it would rip away a part of your body because most of your body would go around the fluon (and only a small part of your body would actually go through). Still, you should feel some force keeping you back as the molecules of your body are strongly connected to one another. You feel the same thing when you push a pin into your body.

Is fluonic drive faster than light travel?

No. The objects which move through a fluon, move just as they move without the fluon, that is, move in continuous space. For example, quantum tunnelling may be explained like this: an electron does not jump over space, it moves in a continuous space, but the structure of the space itself is changed. So, objects could move at 1 meter per second through a fluon, yet they would still show up instantly at the destination because for them there is no space between the source and the destination. The length of the space between source and destination is smaller than in normal space, it's simply zero.

Saying that fluons remap the space is as vague as saying "to travel faster than light, you must active the super drive"

Right. Just as saying "there are 4 forces in the Universe" is only a statement. Nobody knows how come they exist, why they exist, or how they have occurred. Of course, there is a difference: we can observe these forces. We can also observe black-holes. One day we might observe fluons.

Maybe quantum tunnelling is a manifestation of fluons. Maybe electrons only appear to jump over space, but they actually go through a fluon.

Maybe the source and destination spaces of a fluon act as a single space and quantum entanglement is a manifestation of two particles which share this space.

Since fluons occur randomly, quantum tunnelling would also have to happen randomly

Since quantum tunnelling happen in specific physical conditions, those conditions could be responsible for the non-random final effect.

What does it mean "continuous space" and "discontinuous space"?

Continuous space is what you know as normal space.

A discontinuity is something like: 1, 2, 3, 20, 21, 22, 7, 8, 9, 10 ... Here you have a discontinuity at 3 because there should be 4 after 3 instead of 20 (and a discontinuity at 7 because there should be 6 before 7 instead of 22). The 20, 21, 22 sequence is the inside of the fluon.

How a fluon can be generated in practice remains a mystery. You have to apply a function on the real space, but how such a function can be "applied" is the missing link. For example, if you apply f(x) = x + 14 in the points 4, 5, 6, they are transformed into 20, 21, 22. This is how the continuity of the space is remapped, and the fluon created.

What happens if there is a discontinuity in space? Would there be a wall?

If there is a discontinuity in the sense f(x) = 1 / (x – 1), when x -> 1 then f(x) would be infinity. But there would be no wall there since infinity can't actually be reached.

What happens if a fluon is a plane (a 2D space)? When an object which moves through the fluon is half way in, can an observer from the destination see inside the object if he looks from behind the fluon?

The continuity of the space which is in front of space S is remapped with the space which is in front of space D. Thus, an observer which looks at the back of space D would see the back of space S.

What is real space?

Real space is something which behaves like the mathematical space of a function (called fluonic function), where the continuity of the space can be remapped (= one part of space can be made continuous with any other part). The result of the remapping is manifesting as a continuous space, named fluon (or fluonic space).